Matematica
IL MIGLIAIO
Osserva cosa succede se a 999 aggiungi 1 unità
con l'abaco:
con il materiale multibase:
Le dieci unità si cambiano con 1 decina, le decine diventano dieci e vanno
cambiate con un migliaio, cioè 1 k !
L’ ADDIZIONE
L’ addizione è l’operazione che mette insieme due o più quantità, aggiunge una
quantità ad un’altra o ad altre.
I termini dell’addizione
660
+ 328
=
988
Addendo
Addendo Somma o Totale
LA
TABELLA DELL’ADDIZIONE
L’addizione, nell’insieme dei numeri naturali, è un‘operazione sempre
possibile. Se aggiungiamo lo zero a qualsiasi altro, la
somma è uguale al numero stesso. Lo zero è l’elemento
neutro dell’addizione.
Le due parti della tabella, separate dalla linea tratteggiata,
sono simmetriche, perciò vale la proprietà
commutativa: cambiando l’ordine degli addendi la somma non cambia.
Questa proprietà si applica nella prova dell’addizione.
Confrontando i numeri nelle caselle gialle si puo’ scrivere:
2 + 3 = 3 + 2 = 5
Come confrontando i numeri nelle caselle verdi si può scrivere:
6+ 4 = 4 + 6= 10
Le proprietà dell’addizione
Proprietà commutativa
150 + 120 + 210 = 480 cambiando l’ordine degli addendi
il
risultato
non cambia.
210 + 150+ 120 = 480
La proprietà commutativa si applica nella prova dell’addizione
Proprietà associativa :
127 + 3 + 40 + 20
=
se al posto di alcuni addendi si
sostituisce la
loro somma il risultato non cambia.
(127+3) + (40+20)
=
130 + 60 = 190
Proprietà dissociativa :
57 + 22 = 79
se a uno o più addendi se ne sostituiscono
altri la
cui somma è uguale all’addendo sostituito il
risultato non cambia.
50 + 7 + 20 + 2 = 79
_
L’elemento neutro dell’addizione è lo 0
LA SOTTRAZIONE
La sottrazione è l’operazione che mette a
confronto due quantità per calcolare la differenza.
I termini della sottrazione
650
-
310
= 340
Minuendo
Sottraendo Resto o Differenza
LA TABELLA DELLA SOTTRAZIONE
La sottrazione è un’operazione non sempre possibile. Se
il sottraendo è zero il risultato è uguale al
minuendo. Se ad un numero togliamo lo stesso numero, il risultato è zero.
Per la sottrazione non vale la proprietà commutativa, le due
parti della tabella non sono simmetriche. Infatti 4- 3= 1 ma 3- 4= NO!
Le proprietà della sottrazione
es. 148 - 18 = 130
Proprietà invariantiva :
(148 + 2 ) - (18 + 2 )
=
150 -
20 =
130 la
differenza tra due numeri non cambia
se ad entrambi si addiziona o si sottrae lo stesso
numero.
oppure
(427 - 2 ) - (
12 - 2 ) =
425
- 10 =
415
L’elemento neutro della sottrazione è lo
0.
LA
MOLTIPLICAZIONE
La moltiplicazione è l’operazione che ripete più
volte la stessa quantità e calcola il totale nonché
l’operazione che permette di scoprire le combinazioni possibili.
I termini della moltiplicazione
45 X 3
=
125
Fattore
Fattore Prodotto
LA TABELLA DELLA MOLTIPLICAZIONE
La moltiplicazione è un’operazione sempre possibile. L’uno è
detto elemento neutro della moltiplicazione perché qualsiasi
numero moltiplicato x 1, dà come risultato il numero a cui viene
moltiplicato.
Le due parti della tabella, separate dalla linea tratteggiata,
sono simmetriche, perciò vale la proprietà
commutativa: cambiando l’ordine dei fattori il prodotto non cambia.
Questa proprietà si applica nella prova della moltiplicazione.
Confrontando i numeri nelle caselle celesti si puo’ scrivere:
4 x 5 = 5 x 4 = 20
Come confrontando i numeri nelle caselle viola si può scrivere:
4 x 7 = 7 x 4= 28
Le proprietà della moltiplicazione
Proprietà commutativa :
5 x 25 =
125
cambiando l’ordine dei fattori il risultato non cambia.
25 x 5 = 125
Proprietà associativa :
5 x 2 x 3 x 9 =
(5x2) x (3x9) =
se
al posto di alcuni fattori si sostituisce il loro
prodotto
il risultato non cambia.
10 x 27 = 270
Proprietà dissociativa :
25 x 14 =
350
se a uno o più fattori se ne sostituiscono
altri il cui
prodotto è uguale al fattore
sostituito il risultato non
25 x 2 x 7 =
350
cambia.
Proprietà distributiva :
6 x 14 = 84
scomponendo un fattore, si può moltiplicare l’altro
fattore per ciascun termine
dell’addizione ( o sottra-
6 x (10 + 4 )
= zione) ed addizionare poi i prodotti
parziali ottenuti.
(6 x 10) + (6 x 4) =
60 +
24 = 84
L’elemento neutro della
moltiplicazione è l’ 1
LA DIVISIONE
La divisione è l’operazione che distribuisce o raggruppa una quantità
in parti uguali.
I termini della divisione:
140
:
15 = 9
(5)
Dividendo
Divisore Quoziente ( o Quoto quando
il resto
quoziente è “esatto”
privo di resto)
LA TABELLA DELLA DIVISIONE
Le proprietà della divisione
Proprietà invariantiva :
es. 150 : 50 = 3
(150 : 10) : (50 : 10) = 15 :
5 =
3
il quoziente fra due numeri non cambia
se entrambi si dividono o si moltiplicano
per
uno stesso numero, diverso da zero.
Oppure
12 : 2 =
( 12 x 2) : (2x 2) =
24 : 4 = 6
Proprietà distributiva :
175 : 25 = 7
scomponendo il dividendo
si può dividere ciascun
(150 + 25) : 25
=
termine della somma (o
della differenza) per il
divisore e poi som mare (o sottrarre) i quozienti
(150:25) + (25:25) = ottenuti
.
6 + 1 = 7
L’elemento neutro della divisione è l’ 1
TUTTI AL LAVORO….

LE FRAZIONI
La maestra chiede ai suoi alunni di frazionare il foglio colorato in 4 parti.
LEGGIAMO LE FRAZIONI….
LE FRAZIONI COMPLEMENTARI
LE FRAZIONI PROPRIE E LE FRAZIONI IMPROPRIE
Le frazioni proprie
Le frazione è propria quando il numeratore è minore (Più piccolo) del denominatore; indica, pertanto, una quantit. Essa è minore dell’unità.
Le frazioni improprie
La frazione è impropria quando il numeratore è maggiore (Più GRANDE) del denominatore; per questo, indica una QUANTITÀ MAGGIORE DELL’INTERO. Essa è maggiore dell’unità.
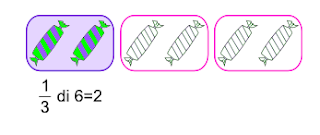
Pertanto, la regola per calcolare la frazione di un numero è formata da due passaggi principali:
· si divide il numero dato per il denominatore;
· successivamente si moltiplica il risultato della divisione effettuata (il quoto) per il numeratore.
1 di 6 = (6 : 2) x 1 = 3 x 1 = 3
3
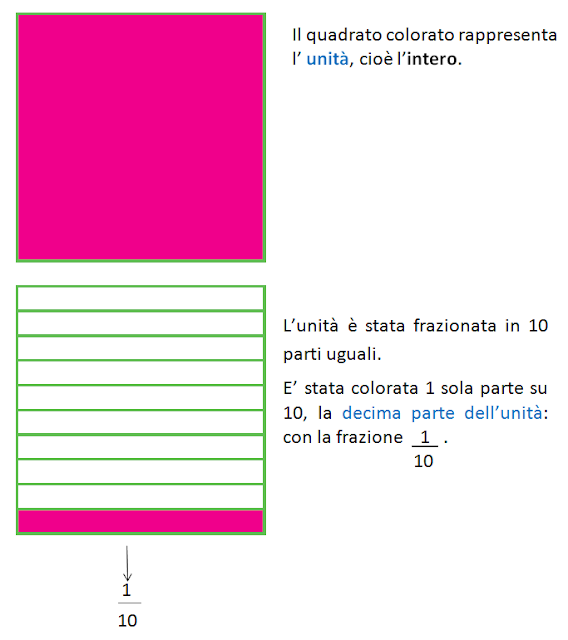
LE FRAZIONI DECIMALI
Le frazioni decimali sono le frazioni che hanno come denominatore 10, 100, 1000.
Osserva e rifletti

In tabella

In tabella
In tabella

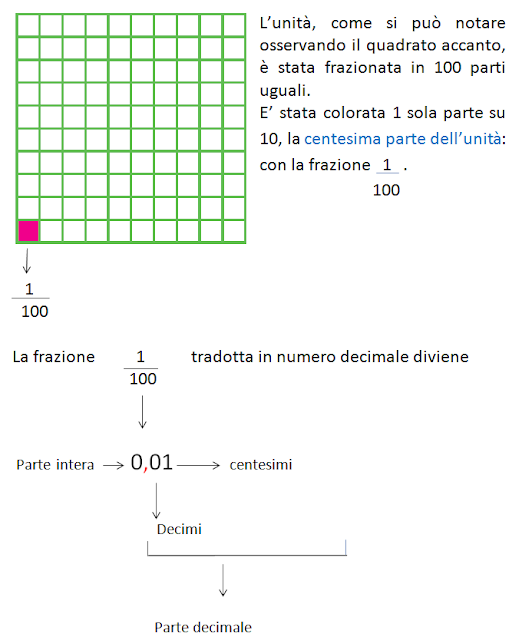
Le frazioni decimali si possono scrivere anche sotto forma di numero con la virgola (numero decimale).
Per separare la parte intera dalla parte decimale si usa la virgola.
VIDEO